A Q&A about using statistics in litigation with David Schwartz, Ph.D., Nathan Schachtman, Esq. moderated by litigation support specialist Ken Lopez
Recently, we posted an article discussing the effective use of trial graphics to help win your cases involving statistical principles. In this prior article, David Schwartz, Ph.D. of Innovative Science Solutions served as a coauthor, helping us to address some fundamental principles related to the use of statistics and hypothesis testing. We ended up the article with a very important question: What can we conclude from studies failing to show statistical significance?
In this article, we attempt to address that important concept in a Q&A with Dr. Schwartz and Nathan A. Schachtman, Esq., an attorney with a nationally recognized legal practice, and who also teaches statistics to law students at Columbia University School of Law. The session was moderated by Ken Lopez, Founder & CEO of A2L Consulting, a national litigation support services firm.
*****************************
Ken Lopez (moderator): Nathan, you reviewed the article that David and I posted about using trial graphics to address some very fundamental principles in statistics?
Nathan Schachtman: Yes, I read your post with great interest; you wrote about issues that are at the heart of what I teach to law students at Columbia.
Moderator: And what do you think about the value of using the right trial graphics provided by a litigation support services firm to teach these principles?
Schachtman: When it comes to teaching judges and jurors, I believe that only graphics will allow us to overcome fear and loathing of mathematics, symbols, and formulae. Trial graphics are extremely important to any attempt to educate non-scientists and scientists alike.
Schwartz: So, Nathan, we want you to help us understand what we can and cannot conclude from data that are not statistically significant. Why is that such an important issue?
Schachtman: Statisticians and careful scientists are well aware of the fallacy of embracing the so-called null hypothesis of no association from a study that has not found a statistically significant disparity. We see the fallacy in the law where it infects some defense counsels' thinking, and some judges' thinking, when they actually conclude no association from a statistically insignificant result. An inconclusive study is, well, inconclusive, and sometimes that is all we can say. Still, even though the burden of proof is typically upon the party claiming the causal effect, we all are very interested to know under what conditions we can say there really is no effect.
Schwartz: So, let’s assume we have a study where we cannot reject the null hypothesis. Let’s say our p-value is 0.2?
Schachtman: That is where the problem starts to arise. Essentially, we can conclude little to nothing from a single study with a p-value in that range. The size of the p-value tells us that a disparity at least as large as we saw between the expected and observed values could well have been the result of chance, assuming there was no difference. We say we have failed to rule out random variability as creating the disparity.
Moderator: Can you give us an example?
Schachtman: Suppose we flip a coin 10 times, and we observe 6 heads and 4 tails. Is this coin lopsided? The answer is "we do not know." The heads/tails ratio observed was 1.5, and that might be the best estimate of the correct, long-term value, but our evidence is very flimsy because of random variation.
Schwartz: Why can't we just accept the null hypothesis? It’s the most likely scenario; right?
Schachtman: No; no; no. The null hypothesis is set as an assumption, and you can't prove an assumption by simply assuming it to be true. The nature of much of statistics, not all, is based upon assuming a so-called null hypothesis, and a reasonable model of probabilistic distribution of events, and asking how likely is it to observe data at least as extreme as we have observed. In many situations, when we obtain an answer that the likelihood of observing data at least as extreme as observed is greater than 5%, we say we cannot reject the starting assumption of no association. Keep in mind that we are talking about the result of a single study, with the p-value greater than 5%.
Schwartz: Many people – scientists and lawyers alike – have transformed this probability into the likelihood of the null hypothesis; haven’t they?
Schachtman: True, they have done that. Any number of courts, expert witnesses, lawyers, litigation support services firms and even published, peer-reviewed articles have stated that a high p-value provides us with the likelihood of the null hypothesis. The mistake is so common, it has a name: “the transpositional fallacy.” The critically important point is that the p-value tells us how likely the data (or the data more extreme) are, given the null hypothesis, and that the p-value does not provide us with a likelihood for the null hypothesis.
Schwartz: But the null hypothesis is what the Defense is really interested in; isn’t it?
Schachtman: The probability of the null hypothesis, or of the observed result, is what everyone in the courtroom is interested in; no question about it. But our desire for an answer of one type doesn’t change the fact that the p-value in traditional hypothesis testing does not allow us to talk about the likelihood of our hypotheses, but only about the likelihood of obtaining the data or data more extreme, given the null hypothesis.
Moderator: Yet people get this wrong all the time, don’t they?
Schachtman: Absolutely. That’s the trap that judges, lawyers, and even statisticians fall into. I’ve written extensively about this on my blog (see this post, for example, where I cite many legal cases where statistical conclusions have been misstated).
Schwartz: Can you give some examples of the types of misstatements you have seen?
Schachtman: In one litigation that I tried to verdict, the federal judge who presided over the pre-trial handling of claims said “P-values measure the probability that the reported association was due to chance… .” See In re Phenylpropanolamine (PPA) Prods. Liab. Litig., 289 F.Supp. 2d 1230, 1236 n.1 (W.D. Wash. 2003). The judge who wrote this incorrect statement was the director of the Federal Judicial Center, which directs the educational efforts of judges on scientific issues. I assure you though that this was not an isolated example of this fallacy.
Schwartz: So, at the end of the day, what can we say about null data? After all, when there are studies showing no difference, the Defense should be able to highlight those studies; shouldn’t they?
Schachtman: Of course. First, let me note that you have now postulated that there are multiple studies that show no difference. Remember, the burden of proof is supposed to be on the plaintiff. So, the defense typically need only show that the plaintiffs cannot prove what they claim. But of course defendants would like, if they can, to go further and interpret the data as showing no association. So multiple null studies do form an important part of the Defense case. But the Defense must be careful not to overstate the conclusions from a single null study. But, as usual, the devil is in the details.
Moderator: What do you mean?
Schachtman: Well, you can actually have a number of different scenarios with respect to null outcomes. Let’s go with the benzene in the fish example that you outlined in your previous blog post. I can think of three interesting scenarios.
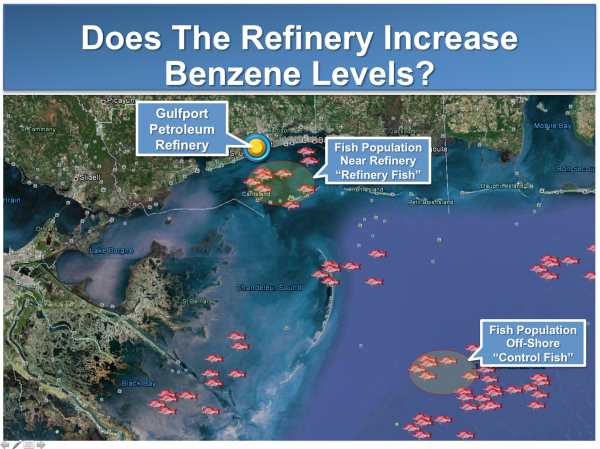
Schachtman: Scenario 1: A single study, with a good deal of random variability, which fails to reject the null with extremely low statistical significance (say, p = 0.4).
Scenario 2: A study with a good deal of statistical precision, which fails to reject the null hypothesis, with marginal statistical significance, say 0.06.
Scenario 3: A series of studies with good statistical precision, each of which fails to reject the null hypothesis.
Schwartz: Why don’t you go through your interpretation of each of the different scenarios you just outlined. Let’s start with Scenario 1, a single, statistically imprecise study, which fails to reject the null hypothesis.
Schachtman: In this scenario, you essentially know very little more than you did before you did the study. You have failed to reject the null hypothesis, but because your study had little statistical precision, the defense cannot really conclude anything about the null hypothesis. To be fair, it would be entirely inappropriate for the plaintiffs to use this example to further their case either. The situation is almost as if the study did not exist. It is very much like my example of flipping a coin 10 times, and observing 6 heads, and 4 tails. We cannot say whether the coin is fair or not fair.
Schwartz: This gets us into the realm of “absence of evidence” vs. “evidence of absence?”
Schachtman: That’s right. Technically, the defense has no burden of proof. If the defense chooses to offer evidence, it may decide to show only that there is no evidence supporting the plaintiff’s case. However, the defense typically wants to go beyond its technical burden and to show that there is affirmative evidence exonerating the defendant; that is, the defense often would like to show the so-called “evidence of absence.”
Moderator: Can you elaborate on that?
Schachtman: If you are going to be statistically correct, you couldn’t argue that this study demonstrated “evidence of absence” – i.e., that Refinery Fish have the same benzene levels as the Control Fish. You flip a coin 10 times, and get 6 heads or 4 tails, do you have a coin that is unfairly weighted, or a fair coin that will yield 50% heads over the long haul? The observation of the 10 flips simply doesn't really help us answer the question. In the example, we simply can’t say whether the Refinery Fish have a higher level of benzene than other fish. We have inconclusive evidence. End of story.
Schwartz: The next Scenario (Scenario 2), a reasonable large, statistically precise study that fails to reject the null with marginal statistical significance, say p = 0.053?
Schachtman: In this case, plaintiffs may be able to argue that although the study didn’t reach statistical significance by the 0.05 standard, it is reasonable to rely on a slightly relaxed standard and to therefore reject the null – i.e., conclude that the Refinery Fish may actually have higher benzene levels than the Control Fish. They would highlight that the 0.05 standard is just a convention and that we shouldn’t slavishly adhere to this standard. The difference between the attained significance probability, 0.053, and the convention, 0.05, is itself not compelling.
Schwartz: And how would the Defense respond?
Schachtman: The Defense would counter that this is the generally accepted standard and that we need some sort of bright line cut-off value. The law needs a "test." Certainly in this type of scenario, it is difficult for the Defense to argue for “evidence of absence”. The defense will want to argue for “absence of evidence” but that becomes difficult the closer the p value is to the conventional 0.05 cut off. If the association is real, then the plaintiffs should not have difficulty obtaining a p-value under 5% by increasing their sample size. One question courts struggle with is whether it is reasonable to insist on a large study to resolve the statistical question.
Schwartz: And the last scenario: a series of reasonably statistically precise studies that each fail to reject the null hypothesis?
Schachtman: Now we are in a scenario where it becomes much more reasonable to argue that we can accept the null hypothesis as a reasonable inference from our data. When a hypothesis has been repeatedly and severely tested, and the tests consistently fail to find no association, there comes a point at which we lose interest in the claim that there is an association, and we embrace a conclusion of no association. After looking under my bed many times, with bigger and bigger flashlights, lasers, motion detectors, and failing to find any communists, I have come to believe that there are no communists under my bed. I sleep much better, and I stop taking my Xanax. Indeed, we have seen this phenomenon of repeated, severe testing leading to the acceptance of no association in a rigorous legal and medical review of the evidence related to silicone breast implants and the risk of systemic autoimmune disease came to this conclusion [see IOM report].
Moderator: Why is it so complicated? We trial graphics and litigation support firms are in the business of simplifying!
Schachtman: A bit too much to go into here. But there has been a lot of writing on this issue, going back at least to the great statistician, Sir Ronald A. Fischer, who refined the notion of significance tests back in the 1920s.
Schwartz: Sometimes the seminal papers are difficult to get through. Anything more modern?
Schachtman: Actually, Sir Ronald wrote with wonderful clarity, and some of his papers are not burdened with a great deal of mathematical formulae. There is a statistician by the name of Sander Greenland, who has dealt with this subject in numerous publications (here is a good example). Of course, the statistics chapter by Law Professor David Kaye, and a very accomplished statistician, the late David Freedman, in the latest edition of the Reference Manual on Scientific Evidence, is an excellent resource.
Schwartz: Is there any way to address the ultimate question? Any way that we can tell a judge or a jury that general causation is so unlikely that it shouldn’t be taken seriously?
Schachtman: Actually, the classic hypothesis testing we have been talking about is called the frequentist model and it was advanced by Sir Ronald Fisher in the 1920s and 1930s. There is a whole other approach to statistical inference, called Bayesian statistics, which theoretically would allow us to offer a probability of belief in the existence of an association. Some disciples of Bayesian statistics complain that the selection of the p-value for statistical significance is arbitrary, but the Bayesian school has its fair share of conceptual problems, as well. But that is a story for another day. I think the important point is that the ultimate question of "how likely is there an association" requires a qualitative synthesis of evidence across studies, and an evaluation of validity within studies.
Schwartz: And, finally, what about causation? You haven’t once mentioned causation.
Schachtman: That is a good point. Because the fish study is based upon observational data – as opposed to randomized or interventional studies -- we haven’t even begun to determine whether we have a reasonable case for causation or whether bias or confounding can better explain the data. Our statistical test addressed only random variability – or the role of chance.
Moderator: What other factors are there?
Schachtman: The two additional factors we must address are bias and confounding. Bias refers to other systematic errors, other than random variation, which threaten the validity of the study. Confounding refers to the presence of a "lurking" variable, which is independently associated with both the exposure and the outcome. Bias and confounding can mask a real relationship; and they can falsely create the appearance of an association. We haven’t even begun to address these. Indeed, bias and confounding can often be much greater threats to the validity of a scientific inference than the role of chance. Stated simply, in evaluating causation from our statistical analyses of random variation in observational studies, we haven’t even gotten off the dime on evaluating causation.
Moderator: And that would involve what?
Schachtman: Some folks would argue that we would have to analyze the available studies under guidelines laid out by Sir Austin Bradford-Hill in his famous address to the Royal Society in 1965. These criteria have come to be known as the Bradford Hill Criteria. Actually, I believe those Bradford Hill guidelines were pretty good for almost 50 years ago, but today we know much more is involved. But as with the Bayesian discussion, that is a story for another day.
Other articles related to teaching statistics or science to juries and judges:









Leave a Comment